If you develop personalization of user experience for your website or an app, contextual bandits can help you. Using contextual bandits, you can choose which content to display to the user, rank advertisements, optimize search results, select the best image to show on the page, and much more.
There are many names for this class of algorithms: contextual bandits, multi-world testing, associative bandits, learning with partial feedback, learning with bandit feedback, bandits with side information, multi-class classification with bandit feedback, associative reinforcement learning, one-step reinforcement learning.
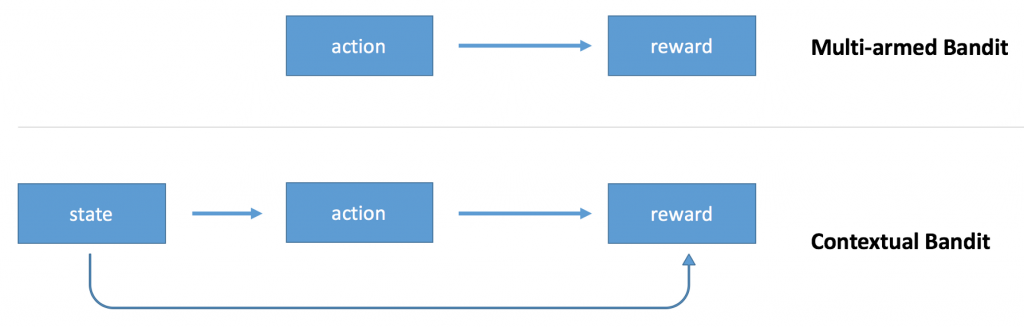
Researchers approach the problem from two different angles. You can think about contextual bandits as an extension of multi-armed bandits, or as a simplified version of reinforcement learning.
“Bandit” in “multi-armed bandits” comes from “one-armed bandit” machines used in a casino. Imagine that you are in a casino with many one-armed bandit machines. Each machine has a different probability of a win. Your goal is to maximize total payout. You can pull a limited number of arms, and you don’t know which bandit to use to get the best payout. The problem involves exploration/exploitation tradeoff: you should balance between trying different bandits to learn more about an expected payout of every machine, but you also want to exploit the best bandit you know about more. This problem has many real-world applications, including website optimization, clinical trials, adaptive routing and financial portfolio design. You can think about it as smarter A/B testing.
The multi-armed bandit algorithm outputs an action but doesn’t use any information about the state of the environment (context). For example, if you use a multi-armed bandit to choose whether to display cat images or dog images to the user of your website, you’ll make the same random decision even if you know something about preferences of the user. The contextual bandit extends the model by making the decision conditional on the state of the environment.
Source: https://medium.com/emergent-future/simple-reinforcement-learning-with-tensorflow-part-0-q-learning-with-tables-and-neural-networks-d195264329d0
With such model, you not only optimize decision based on previous observations, but you also personalize decisions for every situation. You will show an image of a cat to a cat person, and an image of a dog to a dog person, you may show different images at different times of the day and days of the week.
The algorithm observes a context, makes a decision, choosing one action from a number of alternative actions, and observes an outcome of that decision. An outcome defines a reward. The goal is to maximize average reward.
For example, you can use a contextual bandit to select which news article to show first on the main page of your website to optimize click through rate. The context is information about the user: where they come from, previously visited pages of the site, device information, geolocation, etc. An action is a choice of what news article to display. An outcome is whether the user clicked on a link or not. A reward is binary: 0 if there is no click, 1 is there is a click.
If we would have reward values for every possible action for every example, we could just use any classification algorithm, using context data as features and action with the best reward as a label. The challenge is that we don’t know which action is the best, we have only partial information: reward value for the action which was used in the example. You still can use machine learning models for this, but you’ll have to change the cost function. A naïve implementation is to try to predict the reward.
Microsoft published a whitepaper with an overview of the methodology and description of their implementation of a multi-world testing service. This service is being developed by Microsoft Research group in New York. Previously, many of the researchers in that group were working in that field at Yahoo. Microsoft Multi-world testing service uses Vowpal Wabbit, an open source library that implements online and offline training algorithms for contextual bandits. Offline training and evaluation algorithms is described in the paper “Doubly Robust Policy Evaluation and Learning” (Miroslav Dudik, John Langford, Lihong Li).
“Two kinds of approaches address offline learning in contextual bandits. The first, which we call the direct method (DM), estimates the reward function from given data and uses this estimate in place of actual reward to evaluate the policy value on a set of contexts. The second kind, called inverse propensity score (IPS) (Horvitz & Thompson, 1952), uses importance weighting to correct for the incorrect proportions of actions in the historic data. The first approach requires an accurate model of rewards, whereas the second approach requires an accurate model of the past policy. In general, it might be difficult to accurately model rewards, so the first assumption can be too restrictive. On the other hand, it is usually possible to model the past policy quite well. However, the second kind of approach often suffers from large variance especially when the past policy differs significantly from the policy being evaluated.
In this paper, we propose to use the technique of doubly robust (DR) estimation to overcome problems with the two existing approaches. Doubly robust (or doubly protected) estimation (Cassel et al., 1976; Robins et al., 1994; Robins & Rotnitzky, 1995; Lunceford & Davidian, 2004; Kang & Schafer, 2007) is a statistical approach for estimation from incomplete data with an important property: if either one of the two estimators (in DM and IPS) is correct, then the estimation is unbiased. This method thus increases the chances of drawing reliable inference. “
A couple of video tutorials on contextual bandits:
ICML and KDD 2010 Tutorial on Learning through Exploration
And you can find a lot of links to other resources here.
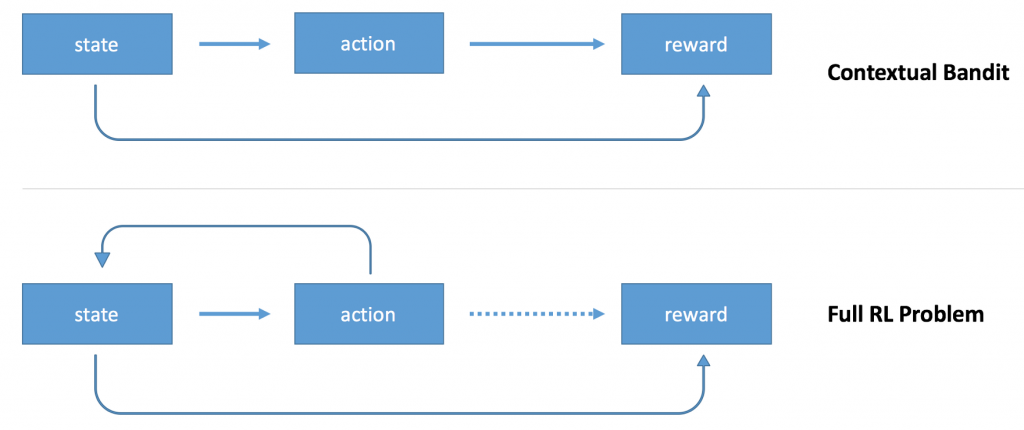
You can think about reinforcement learning as an extension of contextual bandits.
Source: https://medium.com/emergent-future/simple-reinforcement-learning-with-tensorflow-part-0-q-learning-with-tables-and-neural-networks-d195264329d0
You still have an agent (policy) that takes actions based on the state of the environment, observes a reward. The difference is that the agent can take multiple consecutive actions, and reward information is sparse. For example, you can train a model to play chess. The model will use the state of the chess board as context, will decide on which moves to make, but it will get a reward only at the very end of the game: win, loss, or draw. The sparsity of reward information makes it harder to train the model. You encounter a problem of credit assignment problem: how to assign credit or blame individual actions.
There are many variations of reinforcement learning algorithms. One of the extensions of reinforcement learning is deep reinforcement learning. It uses a deep neural network as a part of the system.
Arthur Juliani wrote a nice tutorial on reinforcement learning with Tensorflow.
Researchers interested in contextual bandits seem to focus more on creating algorithms that have better statistical qualities, for example, regret guarantees. Regret is an expected difference between an expectation of the sum of rewards when using an optimal policy and the sum of collected rewards using the contextual bandit policy learned from data. Some classes of algorithms have theoretical guarantees on upper bound of regret.
Researchers interested in reinforcement learning seem to be more interested in applying machine learning algorithms to new problems: robotics, self-driving cars, inventory management, trading systems. They often focus on the development of algorithms that can improve state of the art for some set of problems.
Technical approaches are also different. Microsoft Multiworld Testing Whitepaper describes training algorithm that uses a negative IPS (inverse propensity score) as a loss function. Minimizing the loss function will lead to maximization of IPS estimator. I couldn’t find anybody using IPS estimator in reinforcement learning algorithms. If you get reinforcement learning algorithm with policy gradients and simplify it to a contextual bandit by reducing a number of steps to one, the model will be very similar to a supervised classification model. For the loss function, you will use cross-entropy but multiply by the reward value.
It was interesting to compare two different classes of algorithms which converge in a narrow area of the contextual bandits. I could miss something as I haven’t dig deep into theoretical foundations yet. Please let me know if you notice any mistakes of missing details in this article.